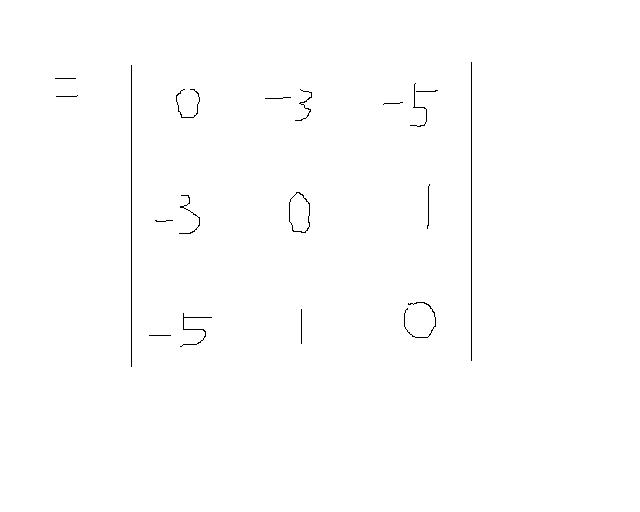라그랑지 함수... 2계조건 헤시안 (Bordered Hessian)

미시경제학(microeconomics)의 소비자이론 중....


Max U= f(x,y)

s.t. g(x,y)=0

즉, g(x,y)의 제약조건하에 f(x,y)를 극대화하는 문제를 생각해 봅니다.

(이미 라그랑지안의 기본에 대해서는 아래 글에서 살펴보았습니다.
http://economia.tistory.com/2       )

이를 라그랑지함수로 나타내면,

L= F(λ,x,y) =f (x,y) + λ(g(x,y))

극대나 극소문제를 확인할 수 있는 일반적인 방법은

경계가 있는 헤시안(Bordered Hessian , = 유테 헤시안, 테두른 헤시안, Hesse 행렬)을 이용한 2계조건을 확인하는 것입니다.

다시말해 라그랑지함수를 통한 해가 극대화를 위한 충분조건(2계조건)을 갖추고 있는지 확인하기 위해서는

Bordered Hessian Determinant(BHD)를 구해봐야 하는데

이 값이 양(+)이어야 합니다. (BHD가 음(-)이면 극소화를 위한 충분조건)

 

        또는 아래와 같이 나타낼 수 있습니다.

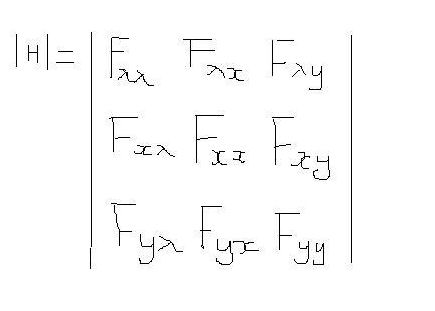
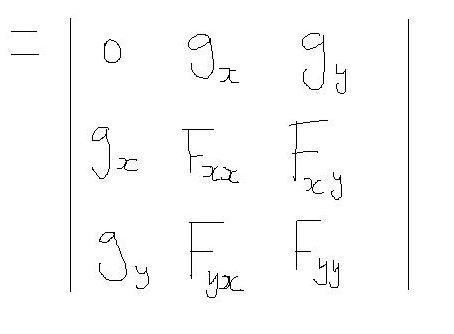
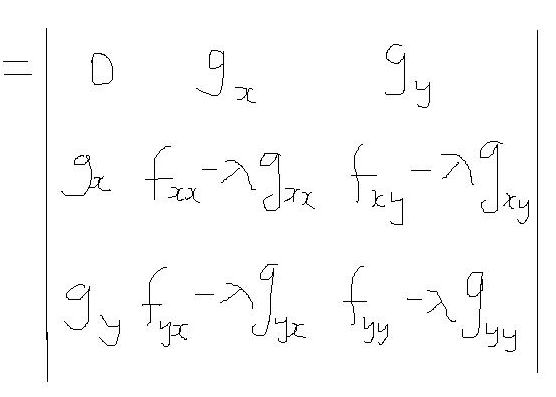
 이를 풀어보면

ㅣH l  

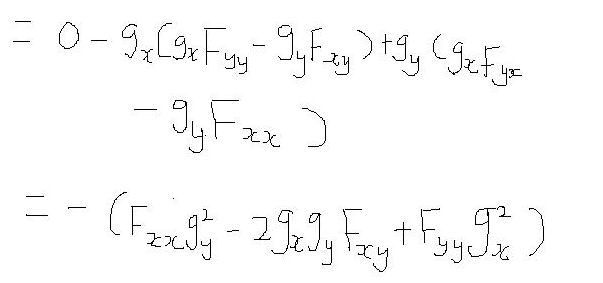
이 값이 양이면 극대화를 위한 2계 충분조건을 갖추고 있는 것으로 확인할 수 있습니다.

<Revisited Example>

max U=xy

     s.t. 3x+5y=90 

L=xy+λ(90-3x-5y)

1계 조건

X에 대해 미분: Lx = Fx= y-3λ=0   -----(1)

y에 대해 미분: Ly = Fy= x-5λ=0  ---(2)

λ에 대해 미분: 90-3x-5y=0 즉, 90=3x+5y ---(3)

(1)---> y=3λ   ---(4)

(2)----> x=5λ  ----(5)

(4),(5)---> (3)에 대입

90=3(5λ)+5(3λ)

90=30λ

λ=3  --->(4),(5)에 대입하면

x=15

y=9

엄밀히 말하면, 이 x,y값은 극값(stationary point)이고, 극대화값인지 극소화값인지는 2계 조건을 구함으로써 알 수 있습니다.

2계 조건인 Bordered Hessian의 값이 양이면 x=15, y=9일 때 효용이 극대화된다는 걸 확인할 수 있게 됩니다.

gx=-3

gy=-5

Fxx=0

Fxy=Fyx=1 (Young's theorem)

Fyy=0

이므로

BHD= l H l =

               = 0 - (-3)(5)-5(-3)

               = 30  > 0

즉,극대화를 위한 2계 충분조건인 Bordered Hessian이 양(+)의 값임을 확인할 수 있으므로

 x=15, y=9 일때 효용이 극대화됩니다.

조금 더 연습이 필요하면 아래를 클릭....

http://userweb.port.ac.uk/~judgeg/SAME/bordered_Hessians.pdf