오일러 정리에 들어가기 전에 k차 동차(homogeneous of degree k)란 말의 의미를 살펴보자.
k차 동차함수란?
만약 f(λx1, λx2,....., λxn) = λ^k f(x1, x2,....., xn) 의 관계가 성립할 때, (다시 그림판으로 써보자)
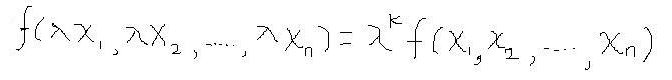
함수 f(x1, x2,....., xn)는 k차 동차(homogeneous of degree k)라 한다.
따라서 함수 f(x1, x2,....., xn)가 1차 동차(homogeneous of degree 1)라 함은
f(λx1, λx2,....., λxn) = λf(x1, x2,....., xn) 일 때 이다.
오일러의 정리(Euler's theorem)란?
함수 f(x1, x2,....., xn)가 k차 동차함수(homogeneous of degree k)라면,
kf(x1, x2,....., xn) = x1(∂f/∂x1) + x2(∂f/∂x2)+ ...... + xn(∂f/∂xn)
<-- 이게 바로 오일러 정리이다.
그 중에서 1차 동차함수(homogeneous of degree 1)라면,
k=1이므로 f(x1, x2,....., xn) = x1(∂f/∂x1) + x2(∂f/∂x2)+ ...... + xn(∂f/∂xn)
경제학에서 오일러 정리가 어떻게 응용되는지 보자.
총생산함수가 1차동차 함수라면 각 생산요소에 대한 지급액이 국민총생산과 일치 한다는 주장은
오일러의 정리로 증명된다.
(생산함수가 1차 동차함수라는 얘기는 규모수익 불변(constant returns to scale)의 특성을 가진다는 뜻이다)
어느 국민경제에 노동(L)과 자본(K)의 두가지 생산요소가 있다고 하자.
즉, 생산함수는 Y=f(L, K)로 표현할 수 있다.
오일러의 정리(K=1일 때)에 의하면 f(x1, x2) = x1(∂f/∂x1) + x2(∂f/∂x2) 이므로
x1, x2 를 L과 K로 바꿔 나타내면
Y = f(L, K) = L(∂f/∂L) + K(∂f/∂K)
양변에 가격 P를 곱하면, PY= PL(∂f/∂L) + PK(∂f/∂K)
좌변은 국민총생산을 의미하고, 우변의 첫번째 항은 노동에 대한 보수를,
두번째 항은 자본에 대한 보수를 나타낸다.
(예를 들어, 첫번째 항이 노동에 대한 보수라는 것을 이해하기 위해서는 임금이
노동의 한계생산가치와 일치한다는 의미를 떠올리면 된다. W=P(∂f/∂L)=P*MPL)
달리 말하면, 생산함수가 규모수익 불변적 특성을 가질 때, 생산요소에 대한 지급총액은 총생산과 일치한다는 의미로, 이때 경제적 이윤은 0이다.
k차 동차함수란?
만약 f(λx1, λx2,....., λxn) = λ^k f(x1, x2,....., xn) 의 관계가 성립할 때, (다시 그림판으로 써보자)
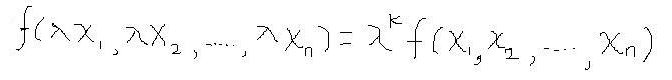
함수 f(x1, x2,....., xn)는 k차 동차(homogeneous of degree k)라 한다.
따라서 함수 f(x1, x2,....., xn)가 1차 동차(homogeneous of degree 1)라 함은
f(λx1, λx2,....., λxn) = λf(x1, x2,....., xn) 일 때 이다.
오일러의 정리(Euler's theorem)란?
함수 f(x1, x2,....., xn)가 k차 동차함수(homogeneous of degree k)라면,
kf(x1, x2,....., xn) = x1(∂f/∂x1) + x2(∂f/∂x2)+ ...... + xn(∂f/∂xn)
<-- 이게 바로 오일러 정리이다.
그 중에서 1차 동차함수(homogeneous of degree 1)라면,
k=1이므로 f(x1, x2,....., xn) = x1(∂f/∂x1) + x2(∂f/∂x2)+ ...... + xn(∂f/∂xn)
경제학에서 오일러 정리가 어떻게 응용되는지 보자.
총생산함수가 1차동차 함수라면 각 생산요소에 대한 지급액이 국민총생산과 일치 한다는 주장은
오일러의 정리로 증명된다.
(생산함수가 1차 동차함수라는 얘기는 규모수익 불변(constant returns to scale)의 특성을 가진다는 뜻이다)
어느 국민경제에 노동(L)과 자본(K)의 두가지 생산요소가 있다고 하자.
즉, 생산함수는 Y=f(L, K)로 표현할 수 있다.
오일러의 정리(K=1일 때)에 의하면 f(x1, x2) = x1(∂f/∂x1) + x2(∂f/∂x2) 이므로
x1, x2 를 L과 K로 바꿔 나타내면
Y = f(L, K) = L(∂f/∂L) + K(∂f/∂K)
양변에 가격 P를 곱하면, PY= PL(∂f/∂L) + PK(∂f/∂K)
좌변은 국민총생산을 의미하고, 우변의 첫번째 항은 노동에 대한 보수를,
두번째 항은 자본에 대한 보수를 나타낸다.
(예를 들어, 첫번째 항이 노동에 대한 보수라는 것을 이해하기 위해서는 임금이
노동의 한계생산가치와 일치한다는 의미를 떠올리면 된다. W=P(∂f/∂L)=P*MPL)
달리 말하면, 생산함수가 규모수익 불변적 특성을 가질 때, 생산요소에 대한 지급총액은 총생산과 일치한다는 의미로, 이때 경제적 이윤은 0이다.
 invalid-file
invalid-file