하나더 풀어보자. 효용함수가 U= (XY)^0.5 인 경우이다. 즉 U = 루트(XY)
이 문제는 다름아닌 콥더글라스 함수로, 혹시 보다 기초적인 내용을 이해하려면 앞의 포스트들을 먼저 살펴보라.
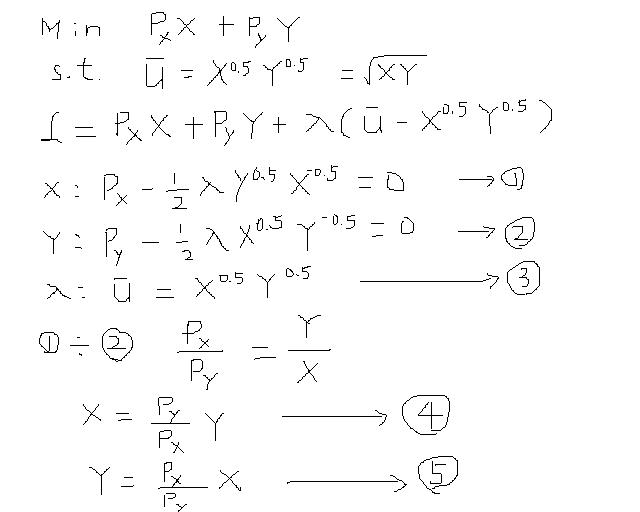


* 일반적인 문제 풀이 순서
예산제약하의 효용극대화 문제를 풀어 구한 X*, Y* (마샬 수요함수, 보통 수요함수)를 U=(XY)^0.5에 대입해서 정리하면
간접효용함수(소득과 가격의 함수)를 구할 수 있고,
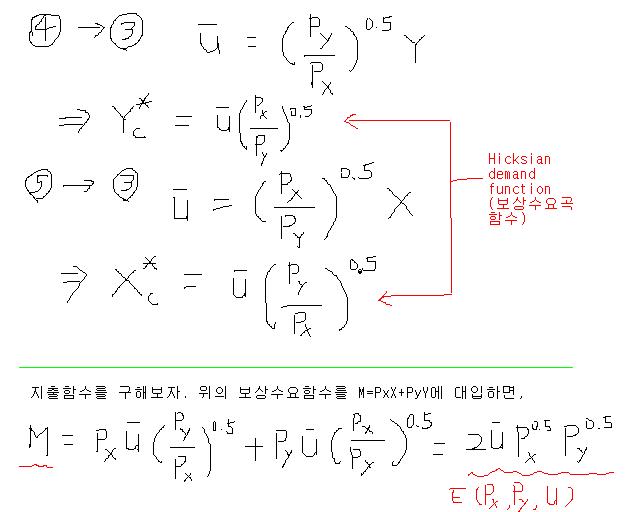
이 간접효용함수를 다시 M에 관하여 풀어 지출함수를 구한다.
이 지출함수를 각 재화의 가격에 관하여 미분하면 (셰파드 보조정리에 의하여) X와 Y의 보상수요함수를 구할 수 있다.
Key Words: 간접효용함수, 지출함수, Shephard's lemma(셰퍼드보조정리), Roy's Identity(로이항등식), 보상수요함수, 쌍대성(Duality)